This is paper is available on arxiv under CC 4.0 DEED license.
Authors:
(1) Leah Chrestien, Czech Technical University in Prague;
(2) Tomá˘s Pevný, Czech Technical University in Prague, and Gen Digital, Inc.;
(3) Stefan Edelkamp, Czech Technical University in Prague;
(4) Antonín Komenda, Czech Technical University in Prague.
Table of Links
- Abstract & Introduction
- Preliminaries
- Conditions on strictly optimally efficient heuristic
- Loss functions
- Related Work
- Experiments
- Conclusion and References
- Appendix
6 Experiments
The experimental protocol was designed to compare the loss functions while removing all sources
of variability. It therefore uses imitation learning in planning [18, 19] and leaves more interesting
bootstrap protocol for future work [3]. The goal was not to deliver state-of-the-art results, therefore
the classical solvers were omitted, but their results are in the Appendix for completeness.

The heuristic function h(s, θ) for a given problem domain was optimized on the training set containing problem instances and their solutions, obtained by SymBA* solver [52] for Sokoban and Maze with teleports and [42] [1] for Sliding Tile. Each minibatch in SGD contained states from exactly a single problem instance needed to calculate the loss. This means that for L2, Lrt, Lle, only states on the solution trajectory were included; for L∗ , Lgbfs, and Lbe there were additional states of distance one (measured by the number of actions) from states on the solution trajectory. Optimized heuristic functions were always evaluated within A* and GBFS forward searches, such that we can analyze how the heuristic functions specialize for a given search. To demonstrate the generality, experiments contained eight problem domains of two types (grid and general PDDL) using two different architectures of neural networks described below.
Neural network for grid domains States in Sokoban, Maze with teleports, and Sliding-puzzle can be easily represented in a grid (tensor). The neural network implementing the heuristic function h(s, θ) was copied from [8]. Seven convolution layers, P1 . . . P7 of the same shape 3 × 3 with 64 filters are followed by four CoAT blocks (CoAT block contains a convolution layer followed by a multi-head attention operation with 2 heads and a positional encoding layer). Convolution layers in CoAT blocks have size 3×3 and have 180 filters. The network to this stage preserves the dimension of the input. The output from the last block is flattened by mean pooling along x and y coordinates before being passed onto a fully connected layer (FC) predicting the heuristic. All blocks have skip connections.
Neural network for PDDL domains For Blocksworld, Ferry, Spanner, N-Puzzle, and Elevators, where the state cannot be easily represented as a tensor, we have used Strips-HGN [44] and we refer the reader therein for details. Strips-HGN was implemented in Julia [4] using PDDL.jl [62] extending [30]. Importantly, we have used the hyper-graph reduplication proposed in [48] to improve computational efficiency. Since we did not know the precise architecture (unlike in the grid domain), we performed a grid-search over the number of hyper-graph convolutions in {1, 2, 3}, dimensions of filters in {4, 8, 16}, and the use of residual connections between features of vertices. The representation of vertices was reduced by mean and maximum pooling and passed to a two-layer feed-forward layer with hidden dimension equal to the number of filters in hyper graph convolutions. All nonlinearities were of relu type. The best configuration was selected according to the number of solved problems in the validation set. Forward search algorithms were given 5s to solve each problem instance chosen in a manner to emphasize differences between loss functions. All experiments were repeated 3 times. All experiments on the PDDL domains including development took 17724 CPU hours. Optimizing heuristic for a single problem instance took approximately 0.5 CPU/h except Gripper domain, where the training took about 8h due to large branch factors. The rest of this subsection gives further details about domains.
Sokoban The training set for the Sokoban domain contained 20000 mazes of grid size 10 × 10 with a single agent and 3 boxes. The testing set contained 200 mazes of the same size 10 × 10, but with 3, 4, 5, 6, 7 boxes. Assuming the complexity of to be correlated with the number of boxes, we can study generalization to more difficult problems. The problem instances were generated by [40].
Maze with teleports The training set contained 20000 mazes of size 15 × 15 with the agent in the upper-left corner and the goal in the lower-right corner. The testing set contained 200 mazes of size 50 × 50, 55 × 55, and 60 × 60. Therefore, as in the case of Sokoban, the testing set was constructed such that it evaluates the generalization of the heuristic to bigger mazes. The mazes were generated using an open-source maze generator [47], where walls were randomly broken and 4 pairs of teleports were randomly added to the maze structure.
Sliding puzzle The training set contained 20000 puzzles of size 5 × 5. The testing set contained 200 mazes of size 5 × 5. These puzzles were taken from [37]. Furthermore, we tested our approach on puzzles of higher dimensions such 6 × 6 and 7 × 7, all of which were generated with [37]. Thus, in total, the testing set contained 200 sliding tile puzzles for each of the three dimensions.
Blocksworld, N-Puzzle, Ferry, Elevators, and Spanner The problem instances were copied from [44] (Blocksworld, N-Puzzle, and Ferry) and from [34] (elevators-00-strips). Problem instances of Spanner were generated by [43]. Blocksworld contained 732 problem instances of size 3–15, N-Puzzle contained 80, Ferry contained 48, Elevators contained 80, and Spanner contained 440. Table 5 in Appendix shows the fraction of -olved mazes by breadth-first search for calibration of the difficulty. The problem instances were randomly divided into training, validation, and testing sets, each containing 50% / 25% / 25% of the whole set of problems. The source code of all experiments is available at https://github.com/aicenter/Optimize-Planning-Heuristics-to-Rank with MIT license.
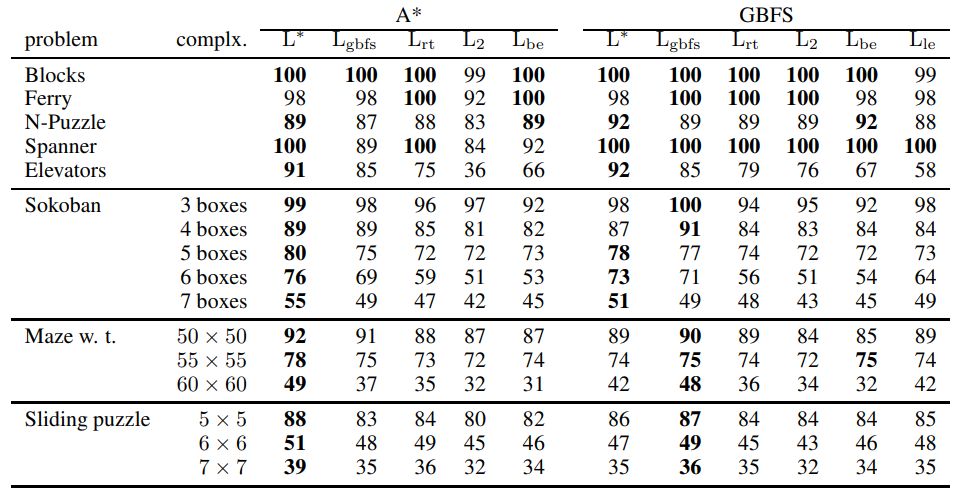
6.1 Experimental results
Table 1 shows the fraction of solved mazes in percent for all combinations of search algorithms (A* and GBFS) and heuristic functions optimized against compared loss functions. The results match the above theory, as the proposed ranking losses are always better than the L2 regression loss.