This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Oded Blumenthal, Software and Information Systems Engineering, Ben Gurion University, Israel;
(2) Guy Shani, Software and Information Systems Engineering, Ben Gurion University, Israel.
Table of Links
- Introduction
- Background
- Related Work
- POMCP for Stochastic Contingent Planning
- Domain Independent Heuristics for POMCP
- Empirical Evaluation
- Conclusion and References
2 Background
We now provide the required background on POMDPs, contingent planning, domain-independent heuristics, and the POMCP algorithm.
2.1 POMDPs

Because the state of a POMDP is partially observable, the agent typically does not know what the true underlying state of the world is. Hence, it can maintain a belief state b, which is a distribution over S, i.e., b(s) is the likelihood that s is the current state. When a goal belief is reached, that is sums∈Gb(s) = 1, then the agent is sure that it is at a goal state, and the execution terminates.
A solution to a POMDP, called a policy, is a function that assigns an action to every belief state. The optimal policy minimizes the expected cost, i.e., the expected number of steps before a goal belief has been reached.
2.2 POMCP
The Partially Observable Monte-Carlo Planning (POMCP) online re-planning approach uses a Monte Carlo tree search (MCTS) approach to select the next action to execute [27]. At each re-planning episode POMCP constructs a tree, where the root node is the current belief state. Then, POMCP runs forward simulations, where a state is sampled from the current belief, and actions are chosen using an exploration strategy that initially selects actions that were not executed a sufficient amount of times, but gradually moves to select the seemingly best action. Observations in the simulations are selected based on the current state-action observation distribution.
When reaching a leaf node, POMCP begins a so-called rollout. This rollout is designed to provide a value estimate for the leaf, based on some predefined rollout policy. The value of the leaf is updated using the outcome of the rollout, and then the values of the nodes along the branch that were visited during the simulation are updated given their descendants. Obviously, the values of all nodes in the tree are hence highly dependent on the values obtained by the rollout policy.
POMCP is an anytime algorithm, that is, it continues to run simulations until a timeout, and then returns the action that seems best at the root of the search tree.
POMCP was designed for large problems. Hence, POMCP does not maintain and update a belief state explicitly. Instead, POMCP uses a particle filter approach, where a set of states is sampled at the initial belief, and this set is progressed through the tree.
2.3 Contingent Planning under Partial Observability

Preconditions allow us to restrict our attention only to applicable actions. An action is applicable in a belief b is all possible states in b satisfy the preconditions of the action. Obviously, one can avoid specifying preconditions for actions, allowing for actions that can always be executed, as is typically the case in flat POMDP representations. However, in domains with many actions, preconditions are a useful tool for drastically limiting the amount of actions that should be considered.
2.4 Regression-based Belief Maintenance
Updating a belief can be costly. Alternatively, one can avoid the computation of new formulas representing the updated belief, by maintaining only the initial belief formula, and the history —the sequence of executed actions and sensed observations [5]. When the agent needs to query whether the preconditions of an action or the goal hold at the current node, the formula is regressed [20] through the action observation sequence back towards the initial belief. Then, one can apply SAT queries to check whether the query formula holds. We now briefly review the regression process for deterministic actions. This approach can be highly useful for larger POMDPs, complementing the particle filter approach used in POMCP.

Regression maintains the equivalence of the formula [20, 5]. For any two formulas φ1 and φ2 we have:
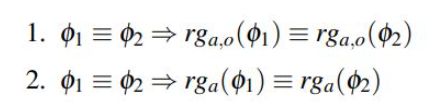
Hence, we can produce a regression over formulas, and compare the regressed formulas, making conclusions about the original formulas.
The regression can be recursively applied to a sequence of actions and observations (history) h as follows:
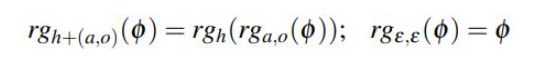
where ε is the empty sequence. This allows us to perform a regression of a formula through an entire plan, and analyze the required conditions for a plan to apply.
In addition, the regression mechanism of [5] maintains a cached list of fluents F(n) that are known to hold at node n, given the action effects or observations. Following an actuation action a, F(a(n)) contains all fluents in F(n) that were not modified by a, as well as effects of a that are not conditioned on hidden fluents. For a sensing action revealing the value l, F(a(n,l)) = F(n) ∪ {l}. During future regression queries, when a value at a particular node becomes known, e.g. when regressing a later observation, it is added to F(n). All fluents p such that p ∈/ F(n)∧ ¬p ∈/ F(n) are said to be hidden at n. The cached list is useful for simplifying future regressed formulas.

