This is paper is available on arxiv under CC 4.0 DEED license.
Authors:
(1) Dhruv Shah, UC Berkeley and he contributed equally;
(2) Michael Equi, UC Berkeley and he contributed equally;
(3) Blazej Osinski, University of Warsaw;
(4) Fei Xia, Google DeepMind;
(5) Brian Ichter, Google DeepMind;
(6) Sergey Levine, UC Berkeley and Google DeepMind.
Table of Links
- Abstract & Introduction
- Related Work
- Problem Formulation and Overview
- LFG: Scoring Subgoals by Polling LLMs
- LLM Heuristics for Goal-Directed Exploration
- System Evaluation
- Discussion and References
- A. Implementation Details
- B. Prompts
3 Problem Formulation and Overview
Our objective is to design a high-level planner that takes as input a natural language query q (e.g., “find the bedside table”), explores the environment in search of the queried object, and commands a low-level policy to control a robotic agent. To do this, we maintain an episodic memory of the environment M in the form of either (i) a 2D map of the environment, where grid cells contain information about occupancy and semantic labels, or (ii) a topological map of the environment, where nodes contain images captured by the robot and corresponding object labels. One way to solve this task is Frontier-Based Exploration (FBE) [31], where a robot maintains a set of unexplored frontiers in it’s memory, and explores randomly to reach the goal. Can we do better with access to LLMs?

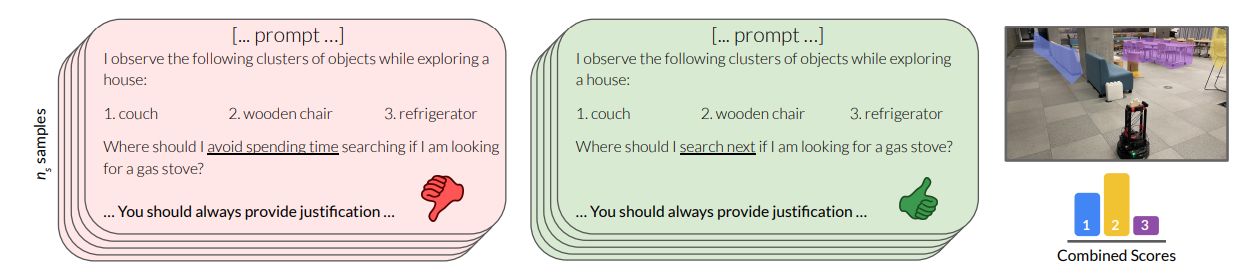
We posit that we can leverage the semantic reasoning capabilities of LLMs by prompting them to construct narratives about which semantic regions of the environment are most (and least) likely to lead to the goal. While the narrative itself might be ungrounded, since the LLM knows very little about the environment, reasoning over objects and semantic regions of the environment often generalizes very broadly. For example, even without seeing a new apartment, a human would guess that the dining area is close to the kitchen. Hence, rather than directly using LLM scores for planning [23, 25], we incorporate them as a goal-directed heuristic to inform the search process. This has two distinct advantages: (i) when the LLM is right, it nudges the search towards the goal, and when it is wrong (or uncertain), we can still default to the underlying FBE algorithm, allowing recovery from LLM failures, and (ii) it allows us to combine the signal from LLMs with other scores that may be more grounded, e.g. distance to subgoals, making the system more versatile.